What's good
Comparing and contrasting with limited sample sizes
Before I jump into this week’s newsletter, I want to remind everyone that at the end of this month I’m giving away 50 percent of whatever I made from premium Substack subscriptions to a randomly selected premium subscriber.
As of today, The F5 has 43 premium subscribers (some opted for the $5/month plan, others the $50/year plan). Clearly, I’m not giving away lifechanging money, but it beats pumping and dumping GME stocks. Get a friend to subscribe and I’ll enter your name in this month’s lottery twice.
In addition to be entered into the monthly lottery, premium subscribers receive the R code used to make the charts in this newsletter every Friday.
Okay, back to the show.
In Los Angeles, Alex Caruso is shooting 55 percent on 3s, or as we say in the analytics community, he’s shooting fire out of his ass. If you sort the 3P% leaderboard on Basketball-Reference.com, Caruso ranks number one overall.
But Caruso has only attempted 33 three-pointers on the season and it would be unfair to compare his three-point percentage to someone like Kentavious Caldwell-Pope’s (shooting 50 percent on 3s), who has taken twice as many attempts. Similarly, it would be just as unfair to compare Pope’s three-point percentage to someone like Paul George’s (48 percent), who has taken twice as many attempts as Pope.
The underlying problem is that because each player has taken a different number of attempts it’s hard to tell which of these three players we ought to be most impressed by. How should we balance the differences in sample sizes (shot attempts) and effect sizes (three-point percentages)?
One common way to address this problem is to only compare players who have taken at least some number of attempts — say 50. But the problem with this approach is that there’s nothing magical about the number 50. It’s arbitrary. Not to mention, it doesn’t solve our secondary problem of trying to compare Pope’s three-point shooting to George’s. Both have taken more than 50 attempts, but is it more impressive to shoot 50 percent on 62 attempts or 48 percent on 124 attempts? And if so, how much more impressive?
Instead of setting an arbitrary threshold which excludes players and throws out useful information, I’ve started comparing players early on in the season by their expected three-point percentage using the “padding method,” which I first read about on Kostya Medvedovsky's blog last summer.
The basic idea behind the padding method is to weigh down (or up) a player’s three-point percentage by the league average and then gradually ease up on that weight as the player increase their three-point attempts. In other words, the padding method assumes a player is more likely to be a league average shooter than not and gradually relaxes that assumption with each increasing shot attempt.
The formula for calculating a player’s expected three-point percentage via the padding method looks like this:
EXPECTED 3P% = (FG3M + X * LEAGUE AVERAGE 3P%) / (FG3A + X)
Whereas the X in the equation is the number that we’re going to use to “pad” the numerator and denominator by, which in this case is 242. That number comes from Medvedovsky’s own research which suggests after 242 attempts, a player's three-point percentage is more “real” than not. Up until 242 attempts, due to the inherent variance of three-point shooting, it’s often safer to assume a player is closer to a league average shooter than not.
To use an example, with the padding method, we would expect Caruso to shoot 38.7 percent on threes the rest of the season, a notch above the league average (36.5 percent), but below Caruso’s actual three-point percentage. Meanwhile, Pope’s expected three-point percentage is 39.3 percent. Once again that’s above league average and below his actual three-point percentage, but the crucial difference is that because Pope has taken more attempts than Caruso, Pope’s expected three-point percentage is further away from the league average.
In the chart below I’ve plotted the actual (solid line) and expected (dotted line) three-point percentages for Caruso, Pope, and George at their corresponding three-point attempt this season.
We can also see that George’s expected three-point percentage is higher than both Caruso’s and Pope’s even though George’s actual three-point percentage is the lowest of the three. In short, we should have more confidence in George being better than a league average shooter at this point in the season than either Caruso or Pope.
What I like about the padding method is that it solves our problem of trying to compare the three-point percentage of players who have taken a different number of attempts. No arbitrary thresholds. No excluding players. It’s not perfect, but it gives us something closer to an apples-to-apples comparison than we had before. The table below shows the ten players with the highest and lowest expected three-point percentage via the padding method so far this season.
Kelly Oubre Jr. has shot the ball so poorly and with so much volume that it’s clear he’s having a worse start to the season than anyone else from behind the three-point line. But even with his cold start, the padding method expects Oubre to shoot a not-great-but-also-not-too-terrible 32.6 percent on 3s the rest of the season. That’s also probably closer to how defenses will treat Oubre. If he really were a 21.8 percent shooter from 3, opposing teams could win games by literally paying Oubre to shoot — although they’re not far off from doing that. Less than three percent of Oubre’s three-point attempts this season have been contested (defense that is either “Tight” or “Very tight”). Only Nikola Vucevic has taken a higher percentage of uncontested looks among the top 50 players in three-point attempts.
The padding method can be used to project all types of stats (free throw percentage, field goal percentage, +/-, etc…), all of which have their own unique padding value that you can find on Medvedovsky’s blog. But I think it’s particularly useful for three-point shooting early on in the season when a single hot (or cold streak) can make a player look better (or worse) than they really are.
League Pass Matchup Of The Night
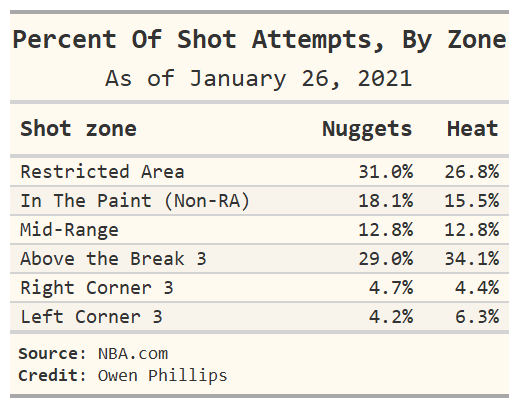
Tonight, the Denver Nuggets play the Miami Heat. The chart (and accompanying table) below shows the areas of the court that each team prefers to take their shots from relative to their opponent.
Relative to Miami, Denver likes to establish themselves in the area near and around the basket. That might not work too well against Miami, who are one of the best rim-protecting teams. The other night in Phoenix, Jokic struggled to score against the mobile and quick-handed Deandre Ayton so I’ll be interested to see how he does against the even more mobile Bam Adebayo.
State Of The MVP Race
After single-handedly dismantling the Cleveland Cavaliers on Monday night, LeBron James now ranks #1 in The F5’s MVP Model. Meanwhile, his odds to win the MVP according the consensus on the Action Network have dropped to +524 (16% implied probability) and trail only Luka Doncic in that respect.
James’ box score stats, while very good, aren’t quite as impressive as Nikola Jokic’s or Doncic’s, but the Lakers are expected to win around 53 games according to FiveThirtyEight, which is five more than anyone else this season. That might end up being the difference maker in a shortened season like this one.
It’s important to emphasize that The F5 MVP Model is trying to predict who will win the MVP and not who should win the MVP (they’re not always the same!). That’s why I’m not that bullish on Joel Embiid’s actual chances of winning the award. His defensive impact isn’t accounted for in The F5 MVP Model, which I think is O.K. given that there aren’t many media members with an MVP vote that I would expect to look beyond offensive box score stats.







Sadly you're completely right with media voting (and tbh fan too)
So you built a model predicting past mvp winners? Sounds interesting
What sort of predictive power does it have?
Did you do categorical regression?